Giải Toán 12 Kết Nối Tri Thức Chương 2 Vectơ Và Hệ Trục Tọa Độ Trong Không Gian
=================
Giải Toán 12 Kết Nối Tri Thức Chương 2 Vectơ Và Hệ Trục Tọa Độ Trong Không Gian
- Giải Toán 12 Kết Nối Tri Thức Bài 6 Vectơ Trong Không Gian
- Giải Toán 12 Kết Nối Tri Thức Bài 7 Hệ Trục Tọa Độ Trong Không Gian
- Giải Toán 12 Kết Nối Tri Thức Bài 8 Biểu Thức Tọa Độ Của Các Phép Toán Vectơ
- Giải Toán 12 Kết Nối Tri Thức Bài Ôn Tập Chương 2
Giải Toán 12 Kết nối tri thức bài 7 Hệ trục tọa độ trong không gian chi tiết dễ hiểu giúp các bạn tham khảo và làm bài tập một cách hiệu quả.
Câu 2.13. Trong không gian $Oxyz$, cho ba vectơ $\vec a,\vec b,\vec c$ đều khác $\vec 0$ và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?
a) Có thể lập một hệ toạ độ Oxyz có các trục toạ độ lần lượt song song với giá của các vectơ $\vec a,\vec b,\vec c$.
b) Có thể lập một hệ toạ độ Oxyz có các trục toạ độ lần lượt trùng với giá của các vectơ $\vec a,\vec b,\vec c$.
c) Có thể lập một hệ toạ độ Oxyz có các vectơ $\vec i,\vec j,\vec k$ lần lượt bằng các vectơ $\vec a,\vec b,\vec c$.
d) Có thể lập một hệ toạ độ Oxyz có các vectơ $\vec i,\vec j,\vec k$ lần lượt cùng phương các vectơ $\vec a,\vec b,\vec c$.
Lời giải
Các mệnh đề đúng là a), d).
Câu 2.14. Hãy mô tả hệ toạ độ $Oxyz$ trong căn phòng ở Hình 2.44 sao cho gốc $O$ trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng $\left( {Oxy} \right)$ và mặt trần nhà trùng với mặt phẳng $\left( {Oxz} \right)$.

Hình 2.44
Lời giải
Trục Ox là mép trần nhà nằm trên bức tường chứa bức tranh, trục Oy là mép còn lại của bức tường chứa bức tranh và trục Oz là mép trần nhà còn lại.
Câu 2.15. Trong không gian $Oxyz$, xác định toạ độ của vectơ $\overrightarrow {AB} $ trong mỗi trường hợp sau:
a) $A\left( {0;0;0} \right)$ và $B\left( {4;2; – 5} \right)$;
b) $A\left( {1; – 3;7} \right)$ và $B\left( {1; – 3;7} \right)$;
c) $A\left( {5;4;9} \right)$ và $B\left( { – 5;7;2} \right)$.
Lời giải
a) $\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right) = \left( {4 – 0;2 – 0; – 5 – 0} \right)$$ = \left( {4;\,\,2;\,\, – 5} \right)$;
b) $\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right) = $$\left( {0;\,\,0;\,\,0} \right)$;
c) $\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right) = $$\;\left( { – 10;\,\,3;\,\, – 7} \right)$.
Câu 2.16. Trong không gian $Oxyz$, xác định toạ độ của điểm $A$ trong mỗi trường hợp sau:
a) $A$ trùng với gốc toạ độ;
b) $A$ nằm trên tia $Ox$ và $OA = 2$;
c) $A$ nằm trên tia đối của tia $Oy$ và $OA = 3$.
Lời giải
a)$A \equiv O(0;0;0) \Rightarrow A(0;0;0)$;
b) $A$ nằm trên tia $Ox$$ \Rightarrow A(a;0;0)$ với $a > 0$
mà $OA = 2$ nên $A\left( {2;\,\,0;\,\,0} \right)$;
c) $A$ nằm trên tia đối của tia $Oy$$ \Rightarrow A(0;b;0)$ với $b
mà $OA = 3$ nên $A\left( {0;\,\, – 3;\,\,0} \right)$.
Câu 2.17. Trong không gian $Oxyz$, cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ có đỉnh $A$ trùng với gốc $O$ và các đỉnh $D,B,A’$ có toạ độ lần lượt là $\left( {2;0;0} \right),\left( {0;4;0} \right),\left( {0;0;3} \right)$ (H.2.45). Xác định toạ độ của các đỉnh còn lại của hình hộp chữ nhật.
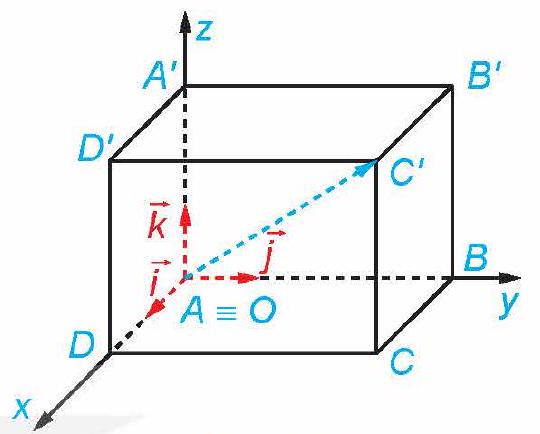
Hình 2.45
Lời giải
+ Tìm tọa độ của đình $A$.
Do $A \equiv O(0;0;0) \Rightarrow A(0;0;0)$
+ Tìm tọa độ của đình $C’$.
Ta có: $\overrightarrow {OC’} = \overrightarrow {OD} + \overrightarrow {OB} + \overrightarrow {OA’} = 2\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k $
$ \Rightarrow C’\left( {2;\,\,4;\,\,3} \right),$
+ Tìm tọa độ của đình $C$.
$\overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OB} = 2\overrightarrow i + 4\overrightarrow j + 0\overrightarrow k $
$ \Rightarrow C\left( {2;\,\,4;\,\,0} \right)$.
+ Tìm tọa độ của đình $B’$.
Ta có: $\overrightarrow {OB’} = \overrightarrow {OB} + \overrightarrow {OA’} = 0\overrightarrow i + 4\overrightarrow j + 3\overrightarrow k $
$ \Rightarrow B’\left( {0;\,\,4;\,\,3} \right)$.
+ Tìm tọa độ của đình $D’$.
$\overrightarrow {OD’} = \overrightarrow {OD} + \overrightarrow {OA’} = 2\overrightarrow i + 0\overrightarrow j + 3\overrightarrow k $
$ \Rightarrow D’\left( {2;\,\,0;\,\,3} \right).$
Câu 2.18. Trong không gian $Oxyz$, cho hình hộp $OABC.O’A’B’C’$ có $A\left( {1;1; – 1} \right),B\left( {0;3;0} \right)$, $C’\left( {2; – 3;6} \right)$.
a) Xác định toạ độ của điểm $C$.
b) Xác định toạ độ các đỉnh còn lại của hình hộp.
Lời giải
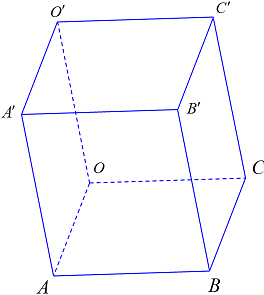
a) Gọi $C(x;y;z)$. Ta có:
$\overrightarrow {OC} = $$(x;y;z)$;
$\overrightarrow {AB} = \left( { – 1;\,\,2;\,\,1} \right)$
Do OABC là hình bình hành nên $\overrightarrow {OC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{gathered}
x = – 1 \hfill \\
y = 2 \hfill \\
z = 1 \hfill \\
\end{gathered} \right.$
suy ra $C\left( { – 1;\,\,2;\,\,1} \right).$
b) * Tìm tọa độ của $O’$.
Ta có $\overrightarrow {OO’} = \overrightarrow {CC’} = \left( {3; – 5;5} \right)$$ \Rightarrow O’\left( {3; – 5;5} \right),$
* Tìm tọa độ của $A’$.
Gọi $A'(x;y;z)$. Ta có: $\overrightarrow {AA’} = \left( {x – 1;y – 1;z + 1} \right)$
Ta lại có: $\overrightarrow {AA’} = \overrightarrow {CC’} = \left( {3; – 5;5} \right)$
$ \Leftrightarrow \left\{ \begin{gathered}
x – 1 = 3 \hfill \\
y – 1 = – 5 \hfill \\
z + 1 = 5 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x = 4 \hfill \\
y = – 4 \hfill \\
z = 4 \hfill \\
\end{gathered} \right.$$ \Rightarrow A’\left( {4; – 4;4} \right),$
* Tìm tọa độ của $B’$.
Gọi $B'(x;y;z)$. Ta có: $\overrightarrow {BB’} = \left( {x;y – 3;z} \right)$
Ta lại có: $\overrightarrow {BB’} = \overrightarrow {CC’} = \left( {3; – 5;5} \right)$
$ \Leftrightarrow \left\{ \begin{gathered}
x = 3 \hfill \\
y – 3 = – 5 \hfill \\
z = 5 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x = 3 \hfill \\
y = – 2 \hfill \\
z = 5 \hfill \\
\end{gathered} \right.$$ \Rightarrow B’\left( {3; – 2;5} \right).$
Câu 2.19. Trong Vận dụng 2 , hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì toạ độ của nó luôn có dạng $\left( {x;y,0} \right)$ với $x,y$ là hai số thực nào đó.
Lời giải
Gọi M là điểm biểu diễn vị trí của máy bay. Khi máy bay di chuyển trên đường băng thì M luôn thuộc mặt phẳng (Oxy), do đó cao độ của M bằng 0. Vì vậy toạ độ của M có dạng $\left( {x;\,\,y;\,\,0} \right).$.
———-

